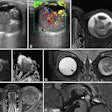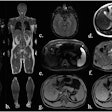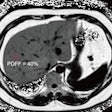
Organs and tumors can twist and turn and otherwise deform substantially during radiotherapy, creating a constantly moving target for treatment planners as they seek to avoid irradiating normal tissues. One solution, a full CT scan before each treatment session, is both time- and radiation-intensive.
But what if doctors could simply "update" the pretreatment CT scan by incorporating a few newly acquired planar projection images into it? After all, much of the anatomic data remains unchanged during the course of treatment, even as other parts are undergoing substantial deformation.
The idea intrigued researchers from the Virginia Commonwealth University School of Medicine in Richmond, VA, who set out to build and test a model that would simulate the deformed anatomy accurately by inserting a minimum of new image data.
It is not an easy task. In the real world, effective image-guided therapy requires large volumes of imaging data to be condensed into an evolving time-dependent 3D picture of the region being treated. New data would have to be incorporated into the old in a way that reflected the true volume of the anatomy.
The model
Alan Docef, Ph.D.; Martin Murphy, Ph.D.; and colleagues from the university's departments of electrical engineering and radiation oncology have succeeded in building such a model. Proof-of-concept tests showed that their simulated deformations were accurate to within a few percentage points of projection radiographs acquired later. At last month's Computer Assisted Radiology and Surgery (CARS) meeting in Berlin, Murphy discussed the group's methods.
"The concept would be to use the initial treatment planning study as a reference or source image, and then take only as much information later as is needed to track changes in the initial CT," said Murphy, who is an associate professor of medical physics at the university. "The way this can be done is to take the initial treatment CT and make a deformable model so that we can change the shape of the planning CT, and make it conform to new data as we acquire it."
Beginning with the high-resolution reference CT data, the team applied a deformation model to move every voxel in the original CT to correspond to the new estimated shape.
"In treatment we have a certain number of projection images. We take the deformable model, we apply it to the original CT, and we make corresponding digitally reconstructed radiographs to compare to the day's projection images," he explained.
Next the attenuation differences between these two sets of data are computed, and the resulting information is plugged back into the deformation model, thereby modifying it to conform to the new data. The process is continued iteratively until a 3D shape is created that conforms to the new projections, Murphy said.
The process produces a fast digital radiograph reconstruction of the type commonly used for the 2D-to-3D rigid registrations to establish anatomic positions. Still, enabling shape changes in soft-tissue anatomy is a more difficult problem requiring many more degrees of freedom, Murphy said.
The researchers used a so-called B-spline deformation model, a piecewise continuous mathematical model of surfaces or volumes that serves as a basis-state representation of the deformation being applied to CT. The model consisted of a mesh (8 x 8 x 8) of control points distributed evenly throughout the volume, with each point serving as a free parameter that can be adjusted (based on the CT attenuation of the new data) to produce a deformation of the source CT that resembles the anatomy as it would appear in a later CT.
"The iteration process adjusts the position of these control points to change the shape of the deformation and consequently change the shape of the anatomy," Murphy said.
The test
So far experiments to verify the model's accuracy have been limited to two numerical proof-of-concept tests, Murphy said. Both were based on 2D simulations and achieved by modeling the deformation of a single axial 2D slice of anatomy, creating one-dimensional fanbeam projections through the slice, and then matching the one-dimensional projections. The synthetic deformation was applied to an actual CT data slice to create an artificial target anatomy.
The deformation applied to the model was relatively smooth and continuous -- not the complex and shifting organ anatomy one might find in some real-world cases, Murphy noted. Still, he said, the resulting shape changes relative to the original CT slice were significant.
The test applied two types of simulated displacement fields to a thoracic CT slice to create the target image. The first field was created using the B-spline model, and was designed to test the model's ability to recover the actual displacement field precisely. The second and more challenging test used a physically realistic deformation to test the algorithm's ability to estimate displacement fields of arbitrary shape.
"We took our synthetic anatomy of the day and created a set of projection images that would represent the conebeam (CT) images taken that day, or in this case, the one-dimensional sinogram slices for that particular day," Murphy said. "And this became our test database. Now our problem was to take the source CT and deform it, and make projections and try to match these target projections."
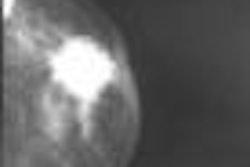
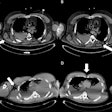
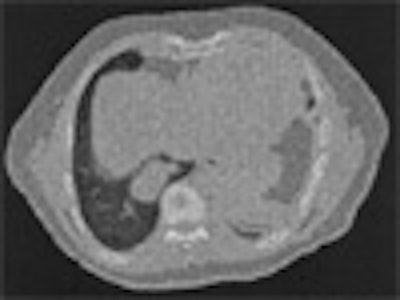
| On the left is one slice of the initial source CT. On the right is the same slice portraying the anatomy at a later time, reconstructed by deforming the source slice, making a synthetic sinogram projection through it, and matching that projection to the sinogram corresponding to the later CT slice. All images courtesy of Michael Murphy, Ph.D. |
First a 2D voxel-by-voxel displacement field was created and applied to the source slice to simulate the later CT. From the deformed target image, 1,500 projections were made and stored to represent the newly acquired target projection data, and the B-spline model was applied to create deformed source images. The gradient-driven iteration sequence was then used to update the deformation model.
Then the 1,500 projections were reduced by a factor of two, and the process was repeated over and over again until just two projections remained. Two projections are known to be sufficient for a six-degrees-of-freedom rigid rotation registration, Murphy noted, but there are many more degrees of freedom in the deformable registration, making the outcome uncertain.
"Can we recover what we put in by creating a synthetic target, and then can we go through our projection matching and recover that using the same baseline concept?" he asked.
Accuracy was measured with two parameters, the difference in the root mean square (RMS) error between the actual and simulated projections, and the difference in the RMS error between the actual and estimated displacement fields.
"If we used as few as eight projections to constrain the deformation model, we got excellent agreement," Murphy said of the results. "We were able to recover and reproduce the deformation model to (0.6%). When we went down to four projections, we could recover it to within 5%, which is good agreement, and when we went all the way down to just two projections, we could recover it to an error of 16%."
In the second test, the team used a harmonic displacement field to deform the thoracic CT slice. Applying the displacement field to the slice and down-sampling it to 64 x 64 pixels made it difficult to estimate the deformation, but the process worked well at 128 x 128 pixels by retaining more of the spatial information needed to constrain the final reconstruction. In this second test, the harmonic displacement field was recovered with approximately the same accuracy as the spline-generated field.
"Our conclusions, based on these proof-of-concept tests in two dimensions, are that if we apply technique to a single slice, a simple one-dimensional sinogram, and if we are faced with simple deformations rather than complex and discontinuous deformations, and if we have a potentially ideal match between actual projections acquired and synthetic (digitally reconstructed radiographs) that we generate, then we can estimate with high accuracy the deformation or the shape of the anatomy of the day with as few as eight projections, and with good accuracy with as few as two projections," Murphy said.
Still, he cautioned, in the real world a digitally reconstructed radiograph never perfectly resembles an actual radiograph, so an important question is what will happen to the accuracy once real radiographs or sinograms are substituted for the synthetic ones. If the method is proved robust in further tests, however, the technique could be useful in a number of applications.
"It gives us a way to register a source CT directly to a conebeam CT through its projections without ever actually reconstructing a conebeam CT," Murphy said. "This has an important value. If the source CT is a fanbeam CT, its Hounsfield numbers are more accurate than the conebeam CT's. And if we follow the fanbeam CT with the conebeam CT and use this technique to morph the fanbeam CT, we can reproduce the deformed anatomy as it is seen in the conebeam CT, but we can preserve the Hounsfield unit numbers accurately from the fanbeam CT."
A potential application, and the focus of this article, is the acquisition of a complete set of conebeam CT data before treatment begins. The data would be modified daily before each session using as few as 10 projections, resulting in significant dose and time savings.
Finally, Murphy said, if the model could be constrained to work with pairs of radiographs taken during a procedure, it could even be used to monitor progress during a single therapy session.
By Eric Barnes
AuntMinnie.com staff writer
July 25, 2005
Related Reading
CARS suite of the future sees key role for image-guided intervention, June 23, 2005
Copyright © 2005 AuntMinnie.com